蒙特卡洛方法

何为蒙特卡洛

其实就是随机采样。蒙特卡洛方法主要用于复杂数值估计，例如核物理方程的数值解（该方法刚被发明出来的时候就是为了解决这个）。现实里还有很多很难找到或者根本找不到解析解的方程（例如计算机图形学的渲染方程），这时候作为数值方法的蒙特卡洛就是求得近似数值解的一种路径。

核心

根据问题域的概率分布反复生成随机数。

例子：估计

是一个无穷级数，我们只能近似估计它。我们可以在此使用蒙特卡洛方法进行估计。

构造一个单位圆 。我们只考虑 的部分，也就是一个边长为 1 的正方形内部的一个四分之一圆。

设一个点 ，如果它在圆的内部，则满足

而四分之一圆的面积： ，正方形的面积：

所以存在以下关系：

所以

C# 实现

正好最近在学 C#，用它来实现一下可以自定义采样数的蒙特卡洛估计器。使用 .NET 自带 Random 类。

class Program
{
    static void Main(string[] args)
    {
        Random rnd = new Random();

        double x, y;

        ulong circleCount = 0;
        
        Console.WriteLine();
        ulong N = Convert.ToUInt64(Console.ReadLine());

        for (ulong i = 0; i < N; i++)
        {
            // 生成随机样本 (x_i, y_i)
            x = rnd.NextDouble();
            y = rnd.NextDouble();

            // 圆内的采样点
            if (x * x + y * y <= 1)
            {
                circleCount++;
            }
        }

        double PI = 4 * (double)circleCount / N;
        
        Console.WriteLine(PI);

    }
}

精度与采样数的关系

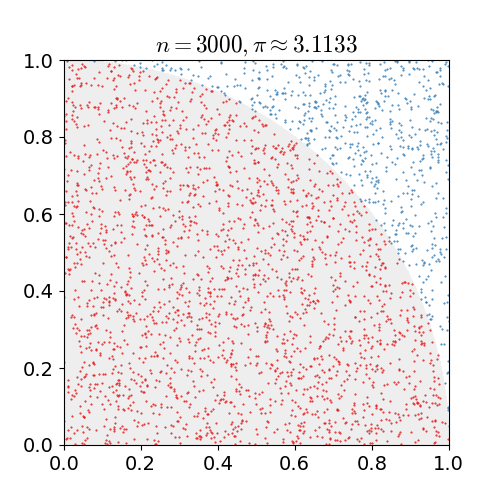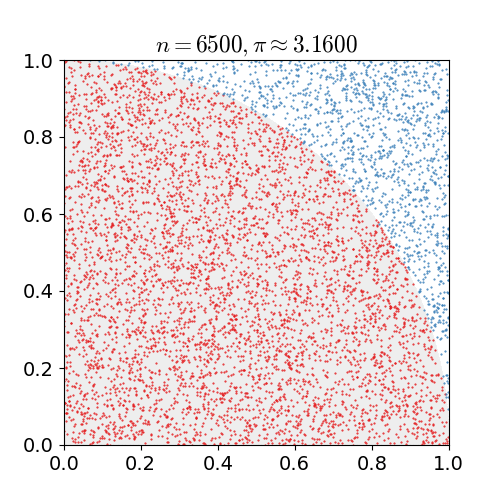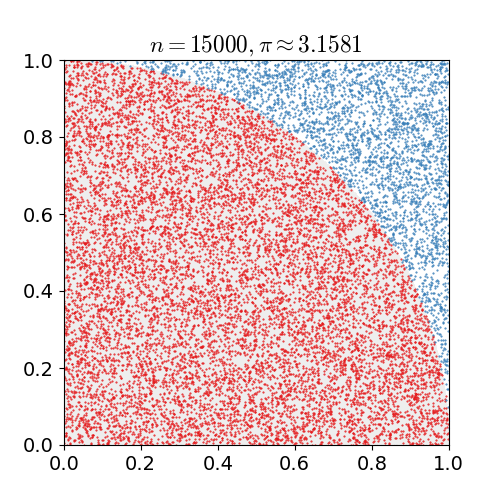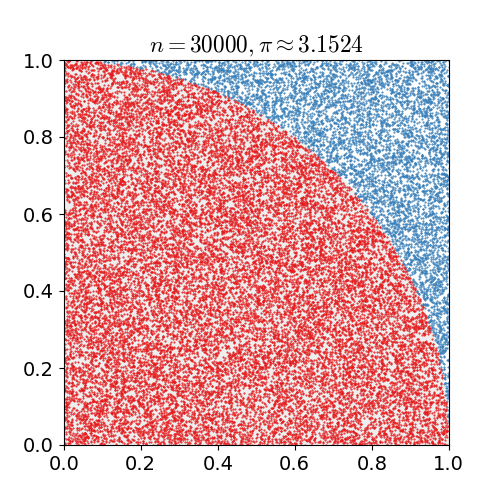
采样数与收敛

我们可以发现， 的精度随采样数的提高而提高。

这在数学上是有解释的，就是样本均值收敛于数学期望，也即概率论学科中大名鼎鼎的大数定律(Law of large numbers)：

名字的由来

蒙特卡洛是摩洛哥的一个著名赌城。